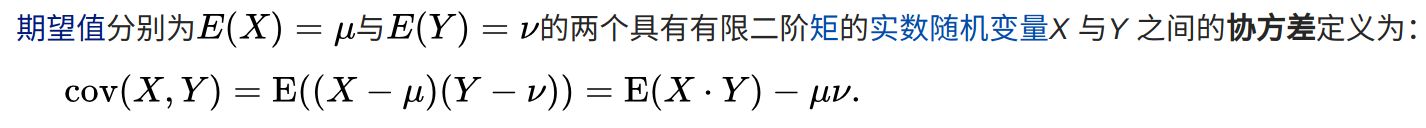算法-PLS(偏最小二乘回归)以及相关概念
线代一窍不通的人开始学习pls… 简单的说，PLSR是PCA、CCA和多元线性回归这三种基本算法组合的产物。
方差
方差（英语：Variance），应用数学里的专有名词。在概率论和统计学中，一个随机变量的方差描述的是它的离散程度，也就是该变量离其期望值的距离。一个实随机变量的方差也称为它的二阶矩或二阶中心动差，恰巧也是它的二阶累积量。这里把复杂说白了，就是将各个误差将之平方（而非取绝对值，使之肯定为正数），相加之后再除以总数，透过这样的方式来算出各个数据分布、零散（相对中心点）的程度。继续延伸的话，方差的正平方根称为该随机变量的标准差（此为相对各个数据点间）。
期望值
在概率论和统计学中，一个离散性随机变量的期望值（或数学期望、或均值，亦简称期望，物理学中称为期待值）是试验中每次可能的结果乘以其结果概率的总和。换句话说，期望值像是随机试验在同样的机会下重复多次，所有那些可能状态平均的结果，便基本上等同“期望值”所期望的数。需要注意的是，期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。（换句话说，期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。） 
例如，掷一枚公平的六面骰子，其每次“点数”的期望值是3.5，计算如下： 
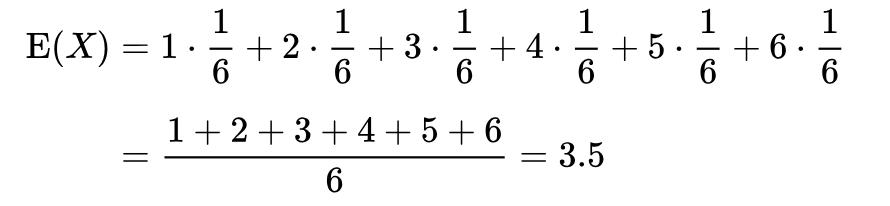不过如上所说明的，3.5虽是“点数”的期望值，但却不属于可能结果中的任一个，没有可能掷出此点数。
协方差
协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。 协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。
协方差矩阵
分别为m 与n 个标量元素的列向量随机变量X 与Y，二者对应的期望值分别为μ与ν，这两个变量之间的协方差定义为m×n 矩阵
两个向量变量的协方差cov(X, Y)与cov(Y, X)互为转置矩阵。
协方差有时也称为是两个随机变量之间“线性独立性”的度量，但是这个含义与线性代数中严格的线性独立性线性独立不同。
PLS2
- 在X矩阵中有很多j变量，(Y中如果是只有一个变量就成为PLS1). 在建模完成后只需要输入X就可以得到Y
- 先对Y进行PCA降维
Y = UQ' + F，因此我们就可以对得分矩阵U进行分析(loading是Q)，进而得到Y 对X也进行PCAX = TP' + E。 - 得到U和Q后可以找到U1=r1×T1 U2=r2×T2, 只要我们得到了T就可以得到U。U1和T1有最大协方差。
- 但是pls不仅仅是pca。如果TU之间没有明显的关系，那么提取再多的组分也无济于事
- 两个关键:必须经常检验U和T的线性关系。记得剔除奇异点。
算法实现
- 第一步: 数据输入，预处理
- 共N个样本对，一个X（N×m）一个Y（N×n），标准化，减均值，做标准差等等。
- 第二步:
- 设X第一个主成分轴向量w1，Y第一个主成分轴向量c1(均为单位向量)，记住两个向量并不是由PCA算出，接下来会具体求解。则由w1,c1可以表示出X，Y的第一对主成分，
t1 = X * w1, u1 = Y * c1. - 综合CCA和PCA的优点，CCA的求解思想是使t1和u1之间的相关性最大化，即Corr(t1,u1)→maxCorr(t1,u1)→max；而PCA的求解思想是分别使t1和u1各自的方差最大，即Var(t1)→max,Var(u1)→maxVar(t1)→max,Var(u1)→max 。综合上面两种思想，即PLSR的求解思想，即Cov(t1,u1)=sqrt(Var(t1)Var(u1))Corr(t1,u1)→max 。数学上可以形式化如下：
Maximize<Xw1,Yc1>Maximize<Xw1,Yc1> ， Subject to : ||w1||=1,||c1||=1 - 通过引入拉格朗日乘子，分别对w1,c1求偏导，可以求得w1 是对称矩阵XTYYTX的最大特征值对应的特征向量，c1是YTXXTY的最大特征值对应的特征向量。
- 这个时候有类似PCA的主成分回归建模
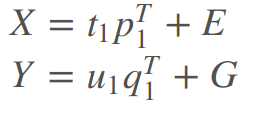
- 上面的p1,q1不同于w1，c1，但是有一定关联，这里利用t1,u1之间的关联性，将Y改为对X的主成分t1进行建模如下。
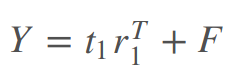
- 对于上述三个回归方程，最小二乘计算p1,q1,r1
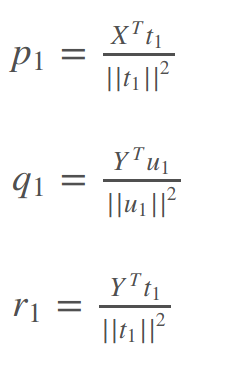
- 上述结果推导出w1,p1关系
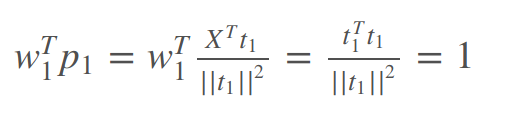
- 设X第一个主成分轴向量w1，Y第一个主成分轴向量c1(均为单位向量)，记住两个向量并不是由PCA算出，接下来会具体求解。则由w1,c1可以表示出X，Y的第一对主成分，
- 第三步
关于一些具体证明键参考文献4
diagnostic
We need some diagnotics to tell us how good the model is.
error measrue
RMSEP^2 = SEP^2(random error) + bias^2(systemetic error)
predict
预测中，X的得分T=XnewP，U=TR，Y=UQ 我们把X的载荷P，R和Q相乘称为B矩阵，我们称之为
regression coefficients
我们将X的第一行与B的第一列相乘得到待预测的Y的第一个组分