2019 April 16 algorithm, external sort

算法-外部排序1

对于太大的数据，无法一次性送入内存，我们就需要进行外部排序。

两个阶段

阶段一

重复将数据从文件读入数组，并用内部排序算法对数组进行排序，然后将数据从数组输出到一个临时文件中。但是这个数组的最大尺寸将依赖于操作系统给JVM分配的内存大小。假定数组最大尺寸为100000个int值，那么临时文件中就是对100000个int值进行排序。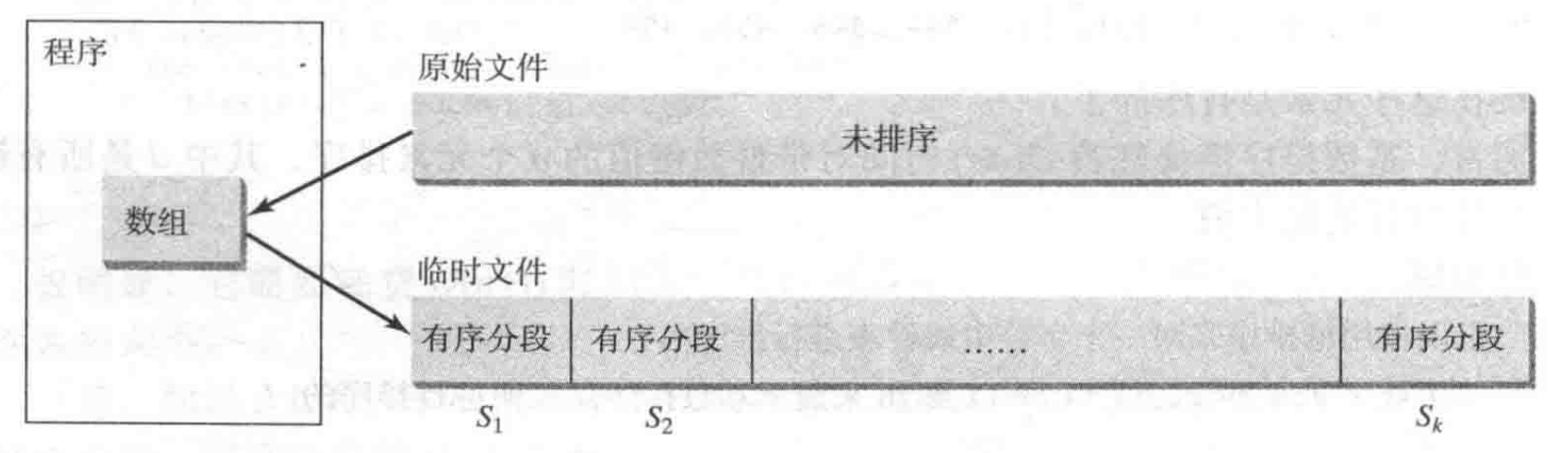

阶段二

将每对有序分段(比如S1和S2，S3和S4…)，归并到一个大一些的有序分段中，并将新分段存储到新的临时文件中。继续同样的过程直到得到仅仅一个有序分段。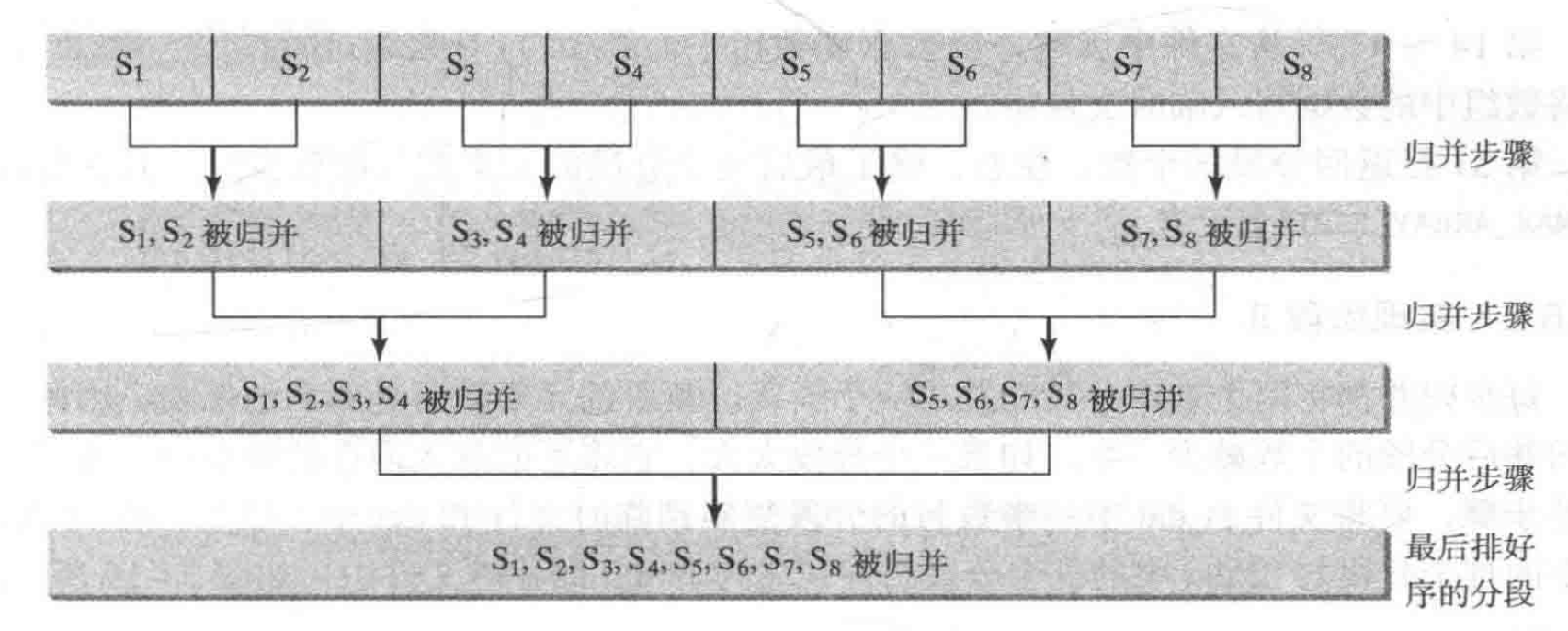

实现阶段1

首先从文件中读取每个数据段，并对分段进行排序，然后将排序好的分段存在新文件中。

/** Sort original file into sorted segments */
  private static int initializeSegments (int segmentSize, String originalFile, String f1) throws Exception {
    int[] list = new int[segmentSize];
    DataInputStream input = new DataInputStream(new BufferedInputStream(new FileInputStream(originalFile)));
    DataOutputStream output = new DataOutputStream(new BufferedOutputStream(new FileOutputStream(f1)));

    int numberOfSegments = 0;
    while (input.available() > 0) {
      numberOfSegments++;
      int i = 0;
      for ( ; input.available() > 0 && i < segmentSize; i++) {
        list[i] = input.readInt();
      }

      // Sort an array list[0..i-1]
      java.util.Arrays.sort(list, 0, i);

      // Write the array to f1.dat
      for (int j = 0; j < i; j++) {
        output.writeInt(list[j]);
      }
    }

    input.close();
    output.close();
    return numberOfSegments;
  }

实现阶段2

每次归并都将两个有序分段归并成一个新段，数目为原来的两倍。因此每次归并后的分段个数将减少一半。如果一个分段太大，将不能放入内存的数组中，为实现归并操作，将f1.dat中一般数目的分段复制到临时文件f2.dat中。然后将f1.dat中的首个分段和f2.dat中的首个分段归并到f3.dat的临时文件中。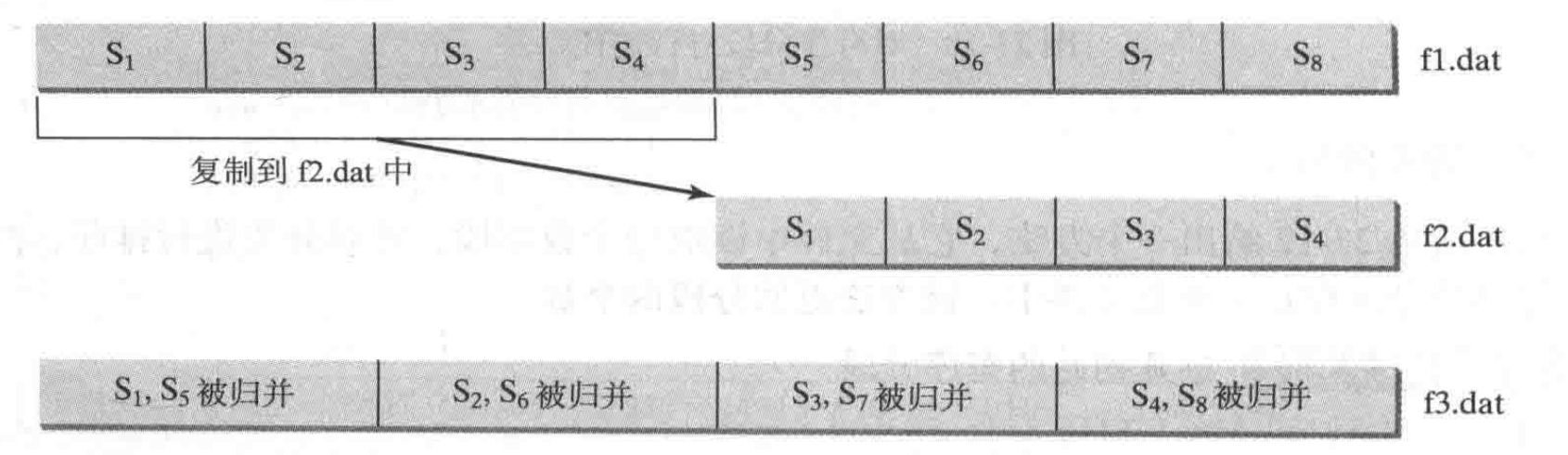

如果f1.dat比f2.dat多一个分段的话，就在归并后将最后一个分段移至f3.dat中

  /** Copy first half number of segments from f1.dat to f2.dat */
  private static void copyHalfToF2(int numberOfSegments,
      int segmentSize, DataInputStream f1, DataOutputStream f2)
      throws Exception {
    for (int i = 0; i < (numberOfSegments / 2) * segmentSize; i++) {
      f2.writeInt(f1.readInt());
    }
  }

  /** Merge all segments */
  private static void mergeSegments(int numberOfSegments,
      int segmentSize, DataInputStream f1, DataInputStream f2,
      DataOutputStream f3) throws Exception {
    for (int i = 0; i < numberOfSegments; i++) {
      mergeTwoSegments(segmentSize, f1, f2, f3);
    }

    // f1 may have one extra segment, copy it to f3
    while (f1.available() > 0) {
      f3.writeInt(f1.readInt());
    }
  }

  /** Merges two segments */
  private static void mergeTwoSegments(int segmentSize,
    DataInputStream f1, DataInputStream f2,
    DataOutputStream f3) throws Exception {
    int intFromF1 = f1.readInt();
    int intFromF2 = f2.readInt();
    int f1Count = 1;
    int f2Count = 1;
  
    while (true) {
      if (intFromF1 < intFromF2) {
        f3.writeInt(intFromF1);
        if (f1.available() == 0 || f1Count++ >= segmentSize) {
          f3.writeInt(intFromF2);
          break;
        }
        else {
          intFromF1 = f1.readInt();
        }
      }
      else {
        f3.writeInt(intFromF2);
        if (f2.available() == 0 || f2Count++ >= segmentSize) {
          f3.writeInt(intFromF1);
          break;
        }
        else {
          intFromF2 = f2.readInt();
        }
      }
    }
  
    while (f1.available() > 0 && f1Count++ < segmentSize) {
      f3.writeInt(f1.readInt());
    }
  
    while (f2.available() > 0 && f2Count++ < segmentSize) {
      f3.writeInt(f2.readInt());
    }
  }
  

复杂度分析

外部排序的主要开销在IO上。假设n是需要排序的个数。

阶段1: 从原始文件读取n个元素，将其输出到临时文件需要花费O(n).
阶段2: 第一个分段结束后，排序好的个数为n/c, c是MAX_ARRAY_SIZE。每个合并步骤都会使得分段的个数减半。所以总共需要log(n/c)次合并。每次合并的过程中，从f1读取一半数量的分段，写入零时文件f2，合并f1和f2中剩下的分段。每一个合并操作I/O次数为O(n),因此I/O总数为: O(n) * log(n/c) = O(nlogn).

reference

Java程序语言设计第十版

点击下载完整代码