2019 April 26 algorithm, external sort

算法-外部排序2

上一次对外部排序的描述似乎太过粗糙了，这次在看了几篇博文以及相关算法书后，再来完善一下。

概览

因为置换排序中的主要矛盾是IO数，因此尽量减少IO次数可以大幅度提升程序运行效率。而减少IO次数主要体现在两个方面。

一方面是使顺串的数量变少(单个顺串的长度变长)
采用多路归并(多相归并) 其中选择置换法网上都是采用败者树实现，但是从算法来说，堆和败者树的时间复杂度和空间复杂度没有什么本质的区别，因此直接采用java.util库中的PriorityQueue来实现比较方便。多路归并就是多划分归并段，具体的就不细说了。

选择置换法

选择置换法可以是的内存一次性能产生相当于数组大小两倍的顺串。

这个算法是在第一阶段划分归并段的时候使用的，相当于可以产生大于数组大小的归并段。证明此结论的方法是 E.F.Moore（人名）在 1961 年从置换—选择排序和扫雪机的类比中得出的，有兴趣的可以自己了解一下。

算法的具体过程

假设内存中只有一个能容纳N个整型的数组
1. 首先从输入文件中读取N个数字将数组填满　　
2. 使用数组中现有数据构建一个最小堆
3. 重复以下步骤直到堆的大小变为0：
　　　　1. 把根结点的数字A（即当前数组中的最小值）输出
　　　　2. 从输入文件中再读出一个数字B，若R比刚输出的数字A 大，则将B放到堆的根节点处，
	若B不比A大，则将堆的最后一个元素移到根结点，将B放到堆的最后一个位置，
	并把堆的大小缩减1（即新读入的数据没有进入堆中）
　　　　3. 在根结点处调用Siftdown重新维护堆
4. 换一个输出文件，重新回到步骤（2）

注意

采用置换选择排序的话，归并段的划分就不能采用直接等分的方法。

采用Huffman树优化各个置换段的归并顺序

由于各个置换段的长度是不一致的，因此在采用多路归并的时候归并顺序会对IO总次数造成影响。现有通过置换选择排序算法所得到的 9 个初始归并段，其长度分别为：9，30，12，18，3，17，2，6，24。在对其采用 3-路平衡归并的方式时可能出现如下图所示的情况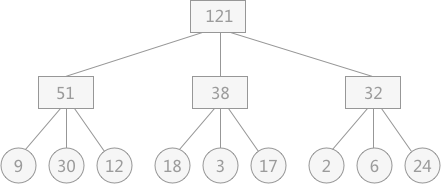：假设在进行平衡归并时，操作每个记录都需要单独进行一次对外存的读写，那么图 1 中的归并过程需要对外存进行读或者写的次数为： (9+30+12+18+3+17+2+6+24）*2*2=484（图中涉及到了两次归并，对外存的读和写各进行 2 次）

可以通过构建Huffman树的方式使根节点的带权路径最短。

如下图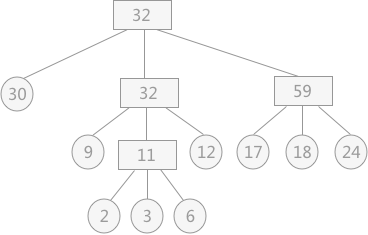其对外存的读写次数为： (2*3+3*3+6*3+9*2+12*2+17*2+18*2+24*2+30)*2=446

二叉的Huffman生成思路

假设每个归并段的字数为C。算法对一个由树组成的森林进行。首先我们需要一个full tree(所有的节点或者是树叶或者有两个儿子)，一个树的权等于他所有树叶归并段长度的和。任意选取最小权的两棵树T1，T2，并任意形成以这两个树为子树的新树，将这样的过程进行C - 1次。算法的开始有C棵单节点树，算法结束后得到一棵树，就是霍夫曼树。

具体过程可以通过一个优先队列实现。对元素个数不超过C的优先队列进行1次BuildHeap，2C - 2次DeleteMin和C - 2次Insert。运行时间为Clog(C),

多路归并

对于外部排序算法来说，其直接影响算法效率的因素为读写外存的次数，即次数越多，算法效率越低。若想提高算法的效率，即减少算法运行过程中读写外存的次数，可以增加 k –路平衡归并中的 k 值。

如果毫无限度地增加 k 值，虽然会减少读写外存数据的次数，但会增加内部归并的时间，得不偿失。

对于 10 个临时文件，当采用 2-路平衡归并时，若每次从 2 个文件中想得到一个最小值时只需比较 1 次；而采用 5-路平衡归并时，若每次从 5 个文件中想得到一个最小值就需要比较 4 次。以上仅仅是得到一个最小值记录，如要得到整个临时文件，其耗费的时间就会相差很大。

为了避免在增加 k 值的过程中影响内部归并的效率，在进行 k-路归并时可以使用“败者树”来实现，该方法在增加 k 值时不会影响其内部归并的效率。败者树是堆排序的一种变形。

多相归并

在有些情况下，多相归并比较好用。对于k路归并，多路归并需要K文件，多相归并只需要3个，但是会增加IO次数，每次都要将文件的一般复制到一个空的文件中。

Polyphase merge sort

英文的Wiki上有较为详细的说明。

After the initial distribution, an ordinary merge sort using 4 files will sort 16 single record runs in 4 iterations of the entire dataset, moving a total of 64 records in order to sort the dataset after the initial distribution. A polyphase merge sort using 4 files will sort 17 single record runs in 4 iterations, but since each iteration but the last iteration only moves a fraction of the dataset, it only moves a total of 48 records in order to sort the dataset after the initial distribution. In this case, ordinary merge sort factor is 2.0, while polyphase overall factor is ~2.73.

To explain how the reduction factor is related to sort performance, the reduction factor equations are:

reduction_factor = exp(number_of_runs*log(number_of_runs)/run_move_count)
run_move_count = number_of_runs * log(number_of_runs)/log(reduction_factor)
run_move_count = number_of_runs * log_reduction_factor(number_of_runs)

Using the run move count equation for the above examples:

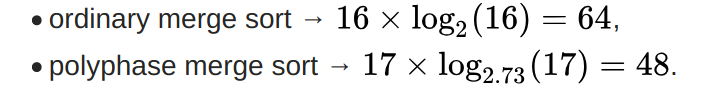Here is a table of effective reduction factors for polyphase and ordinary merge sort listed by number of files, based on actual sorts of a few million records. This table roughly corresponds to the reduction factor per dataset moved tables shown in fig 3 and fig 4 of polyphase merge sort.pdf

# files
|     average fraction of data per iteration
|     |     polyphase reduction factor on ideal sized data
|     |     |     ordinary reduction factor on ideal sized data
|     |     |     |
3     .73   1.94  1.41  (sqrt  2)
4     .63   2.68  2.00
5     .58   3.20  2.45  (sqrt  6)
6     .56   3.56  3.00
7     .55   3.80  3.46  (sqrt 12)
8     .54   3.95  4.00
9     .53   4.07  4.47  (sqrt 20)
10    .53   4.15  5.00
11    .53   4.22  5.48  (sqrt 30)
12    .53   4.28  6.00
32    .53   4.87 16.00

In general, polyphase merge sort is better than ordinary merge sort when there are less than 8 files, while ordinary merge sort starts to become better at around 8 or more files.